- 码距:就单个编码A:00而言,其码距为1,因为其只需要改变一位就变成另一个编码。在两个编码中,从A码到B码转换所需要改变的位数称为码距,如A:00要转换为B:11,码距为2。一般来说,码距越大,越利于纠错和检错。
奇偶校验码
-
奇偶校验码:在编码中增加1位校验位来使编码中1的个数为奇数(奇校验)或者偶数(偶校验),从而使码距变为2。一个合法的奇校验的编码改变成为另一个合法的奇校验编码最少改变两位才可,所以码距为2。例如:
-
奇校验:编码中,含有奇数个1,发送给接收方,接收方收到后,会计算收到的编码有多少个1,如果是奇数个,则无误,是偶数个,则有误。
-
偶校验同理,只是编码中有偶数个1,由上述,奇偶校验只能检1位错,并目无法纠错。
CRC校验码
- CRC只能
检错,不能纠错。使用CRC编码,需要先约定一个生成多项式G(x)。生成多项式的最高位和最低位必须是1。假设原始信息有m位,则对应多项式M(x)。生成校验码思想就是在原始信息位后追加若干校验位,使得追加的信息能被G(x)整除。接收方接收到带校验位的信息,然后用G(x)整除。余数为0,则没有错误;反之则发生错误。
例:假设原始信息串为10110,CRC 的生成多项式为G(x)=x^4+x+1,求CRC 校验码。
-
在原始信息位后面添0,假设生成多项式的阶为r,则在原始信息位后添加r个,本题中,G(x)阶为4,则在原始信息串后加4个0,得到的新串为101100000,作为被除数。
-
由
多项式得到除数,多项中的幕指数存在的位置1,不存在的位置0。本题中,×的幕指数为0,1,4的变量都存在,而幕指数为2,3的不存在,因此得到串10011. -
生成CRC校验码,将前两步得出的被除数和除数进行
模2除法运算(异或,同0异1,即不进位也不借位的除法运算)。除法过程如下图所示。得到余数1111。注意:余数不足r,则余数左边用若干个0补齐。如求得余数为11,r=4,则补两个得到0011。
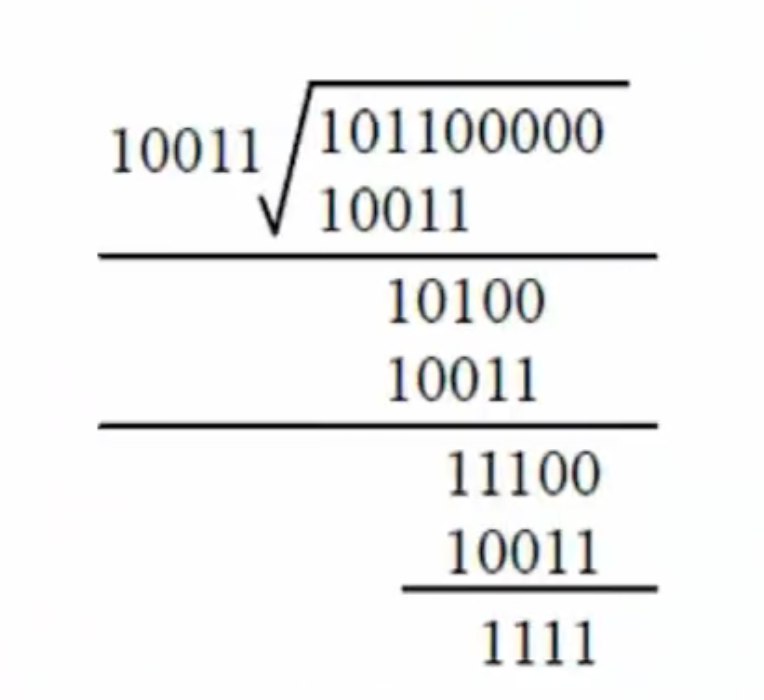
-
生成最终发送信息串,将余数添加到原始信息后。上例中,原始信息为10110,添加余数1111后,结果为10110 1111。发送方将此数据发送给接收方。
-
接收方进行校验。接收方的CRC 校验过程与生成过程类似,接收方接收了带校验和的帧后,用多项式G(x)来除。余数为0,则表示信息无错;否则要求发送方进行重传。
注意:收发信息双方需使用相同的生成多项式。